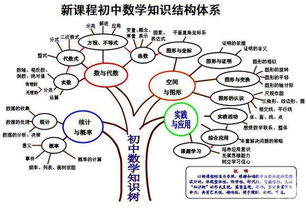
混
合课代数 在数学中，我们通常将代数和几何作为两个独立的学科来学习。但实际上，它们之间有许多共同之处。学习交点、切线以及非线性方程等内容可以帮助我们更好地理解代数与几何之间的联系。 举个例子，我们通常认为，一条直线可以由y=ax+b的形式来表示。但是，如果我们尝试描述一条非常陡峭的直线（其中a的值非常大），那么这个方程很可能会变得非常复杂。相比之下，我们可以使用几何方法将这些概念形象化。 考虑如何描述直线y=2x+5。我们可以将这条直线画在坐标系上，并将一个点（比如（3,11））与它相连。通过计算斜率并使用标准点斜式，我们可以得到： (y-11)/(x-3) = 2 将其简化后可以得到: y=2x+5 因此，我们可以看到，代数和几何之间的关系实际上是相互促进的关系,互相补足，相得益彰。 五阶方程求解 在代数学中，五次方程是一个非常执着的问题。因为找到这种方程的一般解决方案是不可能的。然而，这并不是说我们不能通过其他方法来解决这个问题。我们可以使用一些其他技术来近似解决五次方程。 例如，我们可以使用牛顿法将其转换为一种方便求解的形式。这个方法的基本思想是指定一个初始值，然后使用一个递推公式来逐渐逼近更精确的解决方案。如果我们使用这种方法来寻找根号3，我们将得到以下递归公式: x_n+1 = (2x_n + 3/x_n^2)/3 将其简化一下，就可以得到： x_n+1 = x_n - (x_n^3 - 3)/(3x_n^2) 使用这个公式，我们可以得到以下近似计算结果： 初值（x0） 等式左边结果 等式右边结果 √3
1.73205080756887729353 2
1.73205110789222177231
1.7320511079
1.7
1.73205093492508178465
1.732050935
1.732
1.73205080790711881259
1.732050808 如上表，我们发现递归逼近后，左右两侧已非常接近，我们可以通过多次重复上述计算，可以更精确地估算出根号3的值。 四维数学 你是否想象过，数学可以距离我们日常生活这么遥远吗？在数学领域中，我们很容易进入到更复杂的领域，如四维数学。 在三维几何学中，我们可以使用箭头来表示向量。在四维情况下，我们就需要使用四个数字来完全描述一个向量。阅读四维数学的时候，我们需要使用更高级的抽象工具，并常常依靠几何直觉来更好地描述相关问题。这样，我们可以更加深入地理解三维世界，并且更好地了解宇宙的本质。 总结 数学中有许多我们耳熟能详、但还没有被深度发掘的有关冷知识。它们通常看起来有些抽象，但却隐藏着不少有趣的概念。 无论是通过混合课代数与几何的方法、近似计算五阶方程的解，还是探讨四维世界的可能性，我们都可以发现，数学世界是深邃而有趣的。它在表达问题的时候或许会有些复杂，但是在理解事物本质之后，它的优美之处便悄悄地呈现出来。让我们一起走进数学的世界，发掘其中的奥秘吧！