轴
对称的冷知识
轴对称是一种常见的几何变换,具有许多有趣的性质和应用。本文将介绍一些与轴对称相关的冷知识,帮助大家更好地理解和应用这一几何变换。
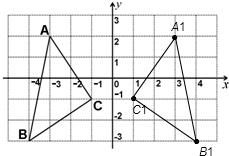
1. 轴对称不改变面积和形状
一个平面图形在进行轴对称变换时,其面积和形状均不变。这是因为轴对称变换只是将每个点关于轴线对称,而不会拉伸、压缩或旋转图形。因此,如果你需要保持面积或形状不变,可以考虑使用轴对称变换。
2. 轴对称可以用于构造对称图形
轴对称变换可以用于构造许多对称图形,如正多边形和星形图案。例如,要构造一个8边形的对称图形,可以先画出一条通过正方形两个对角线交点的对称轴,然后将正方形绕轴对称变换8次,即可得到一个具有8个对称轴的8边形。
3. 轴对称可以用于求解几何问题
轴对称变换可以用于解决许多几何问题,如寻找中垂线、角平分线、对称轴等。例如,如果要寻找一个三角形的垂心(三边垂直的交点),可以先找到三个中垂线,然后通过轴对称变换将它们都交于一点,即可求得垂心。
4. 轴对称可以用于解决数学难题
轴对称变换也可以用于解决许多数学难题,如圆排列、蛇形填数等。例如,如果要将8个相同大小的圆排列成一个正六边形图案,可以先将一个圆固定在六边形中心,然后将其余7个圆依次绕中心逆时针对称变换45度、90度、135度、180度、225度、270度和315度,即可得到一个完整的正六边形图案。
5. 轴对称可以用于制作艺术品
轴对称变换不仅有数学应用,还可以用于创作艺术品。许多艺术家喜欢使用轴对称变换构造对称图案,如莫比乌斯环、对称图案和无限循环图案等。例如,荷兰艺术家艾舍尔就创作了许多以轴对称为特色的画作,如《蜥蜴》和《天使与魔鬼》等。
总之,轴对称是一种非常有用和有趣的几何变换,它们不仅有数学应用,还可以用于科学研究、制作艺术品和解决数学难题等。如果你想更好地理解和应用轴对称变换,可以尝试通过练习、探索和创作来提高自己的能力。
